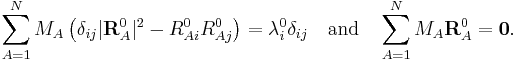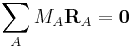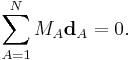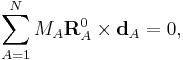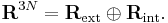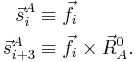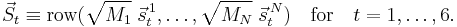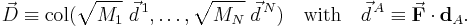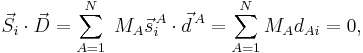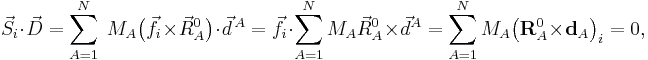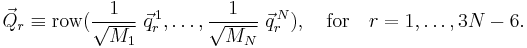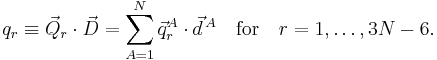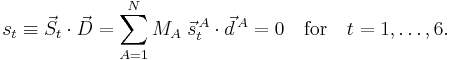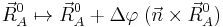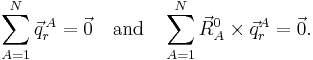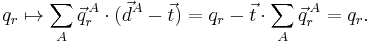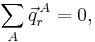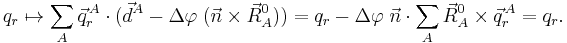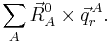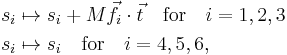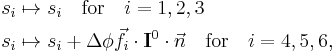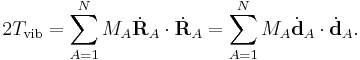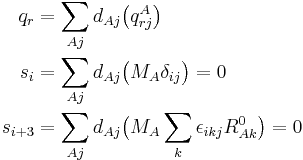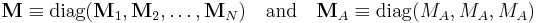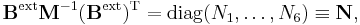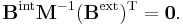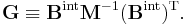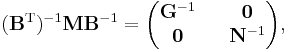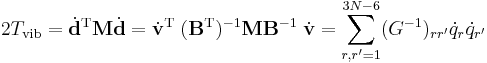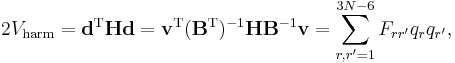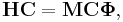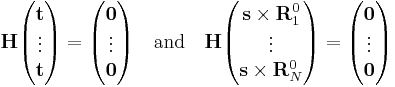Eckart conditions
The Eckart conditions,[1] named after Carl Eckart, sometimes referred to as Sayvetz conditions,[2] simplify the nuclear motion (rovibrational) Schrödinger equation that arises in the second step of the Born-Oppenheimer approximation. The Eckart conditions allow to a large extent the separation of the external (rotation and translation) motions from the internal (vibration) motions. Although the rotational and vibrational motions of the nuclei in a molecule cannot be fully separated, the Eckart conditions minimize the coupling between these two.
Contents |
Definition of Eckart conditions
The Eckart conditions can only be formulated for a semi-rigid molecule, which is a molecule with a potential energy surface V(R1, R2,..RN) that has a well-defined minimum for RA0 (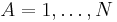 ). These equilibrium coordinates of the nuclei—with masses MA—are expressed with respect to a fixed orthonormal principal axes frame and hence satisfy the relations
). These equilibrium coordinates of the nuclei—with masses MA—are expressed with respect to a fixed orthonormal principal axes frame and hence satisfy the relations
Here λi0 is a principal inertia moment of the equilibrium molecule. The triplets RA0 = (RA10, RA20, RA30) satisfying these conditions, enter the theory as a given set of real constants. Following Biedenharn and Louck[3] we introduce an orthonormal body-fixed frame, the Eckart frame,
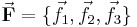 .
.
If we were tied to the Eckart frame, which—following the molecule—rotates and translates in space, we would observe the molecule in its equilibrium geometry when we would draw the nuclei at the points,
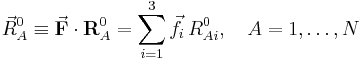 .
.
Let the elements of RA be the coordinates with respect to the Eckart frame of the position vector of nucleus A (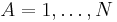 ). Since we take the origin of the Eckart frame in the instantaneous center of mass, the following relation
). Since we take the origin of the Eckart frame in the instantaneous center of mass, the following relation
holds. We define displacement coordinates
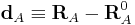 .
.
Clearly the displacement coordinates satisfy the translational Eckart conditions,
The rotational Eckart conditions for the displacements are:
where 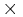 indicates a vector product. These rotational conditions follow from the specific construction of the Eckart frame, see Biedenharn and Louck, loc. cit., page 538.
indicates a vector product. These rotational conditions follow from the specific construction of the Eckart frame, see Biedenharn and Louck, loc. cit., page 538.
Finally, for a better understanding of the Eckart frame it may be useful to remark that it becomes a principal axes frame in the case that the molecule is a rigid rotor, that is, when all N displacement vectors are zero.
Separation of external and internal coordinates
The N position vectors 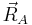 of the nuclei constitute a 3N dimensional linear space R3N: the configuration space. The Eckart conditions give an orthogonal direct sum decomposition of this space
of the nuclei constitute a 3N dimensional linear space R3N: the configuration space. The Eckart conditions give an orthogonal direct sum decomposition of this space
The elements of the 3N-6 dimensional subspace Rint are referred to as internal coordinates, because they are invariant under overall translation and rotation of the molecule and, thus, depend only on the internal (vibrational) motions. The elements of the 6-dimensional subspace Rext are referred to as external coordinates, because they are associated with the overall translation and rotation of the molecule.
To clarify this nomenclature we define first a basis for Rext. To that end we introduce the following 6 vectors (i=1,2,3):
An orthogonal, unnormalized, basis for Rext is,
A mass-weighted displacement vector can be written as
For i=1,2,3,
where the zero follows because of the translational Eckart conditions. For i=4,5,6
where the zero follows because of the rotational Eckart conditions. We conclude that the displacement vector 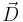 belongs to the orthogonal complement of Rext, so that it is an internal vector.
belongs to the orthogonal complement of Rext, so that it is an internal vector.
We obtain a basis for the internal space by defining 3N-6 linearly independent vectors
The vectors 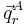 could be Wilson's s-vectors or could be obtained in the harmonic approximation by diagonalizing the Hessian of V. We next introduce internal (vibrational) modes,
could be Wilson's s-vectors or could be obtained in the harmonic approximation by diagonalizing the Hessian of V. We next introduce internal (vibrational) modes,
The physical meaning of qr depends on the vectors 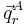 . For instance, qr could be a symmetric stretching mode, in which two C—H bonds are simultaneously stretched and contracted.
. For instance, qr could be a symmetric stretching mode, in which two C—H bonds are simultaneously stretched and contracted.
We already saw that the corresponding external modes are zero because of the Eckart conditions,
Overall translation and rotation
The vibrational (internal) modes are invariant under translation and infinitesimal rotation of the equilibrium (reference) molecule if and only if the Eckart conditions apply. This will be shown in this subsection.
An overall translation of the reference molecule is given by
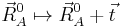 '
'
for any arbitrary 3-vector 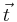 . An infinitesimal rotation of the molecule is given by
. An infinitesimal rotation of the molecule is given by
where Δφ is an infinitesimal angle, Δφ >> (Δφ)², and 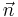 is an arbitrary unit vector. From the orthogonality of
is an arbitrary unit vector. From the orthogonality of 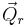 to the external space follows that the
to the external space follows that the 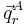 satisfy
satisfy
Now, under translation
Clearly, 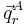 is invariant under translation if and only if
is invariant under translation if and only if
because the vector 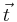 is arbitrary. So, the translational Eckart conditions imply the translational invariance of the vectors belonging to internal space and conversely. Under rotation we have,
is arbitrary. So, the translational Eckart conditions imply the translational invariance of the vectors belonging to internal space and conversely. Under rotation we have,
Rotational invariance follows if and only if
The external modes, on the other hand, are not invariant and it is not difficult to show that they change under translation as follows:
where M is the total mass of the molecule. They change under infinitesimal rotation as follows
where I0 is the inertia tensor of the equilibrium molecule. This behavior shows that the first three external modes describe the overall translation of the molecule, while the modes 4, 5, and, 6 describe the overall rotation.
Vibrational energy
The vibrational energy of the molecule can be written in terms of coordinates with respect to the Eckart frame as
Because the Eckart frame is non-inertial, the total kinetic energy comprises also centrifugal and Coriolis energies. These stay out of the present discussion. The vibrational energy is written in terms of the displacement coordinates, which are linearly dependent because they are contaminated by the 6 external modes, which are zero, i.e., the dA's satisfy 6 linear relations. It is possible to write the vibrational energy solely in terms of the internal modes qr (r =1, ..., 3N-6) as we will now show. We write the different modes in terms of the displacements
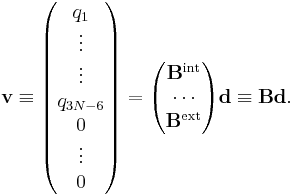
The parenthesized expressions define a matrix B relating the internal and external modes to the displacements. The matrix B may be partitioned in an internal (3N-6 x 3N) and an external (6 x 3N) part,
We define the matrix M by
and from the relations given in the previous sections follow the matrix relations
and
We define
By using the rules for block matrix multiplication we can show that
where G-1 is of dimension (3N-6 x 3N-6) and N-1 is (6 x 6). The kinetic energy becomes
where we used that the last 6 components of v are zero. This form of the kinetic energy of vibration enters Wilson's GF method. It is of some interest to point out that the potential energy in the harmonic approximation can be written as follows
where H is the Hessian of the potential in the minimum and F, defined by this equation, is the F matrix of the GF method.
Relation to the harmonic approximation
In the harmonic approximation to the nuclear vibrational problem, expressed in displacement coordinates, one must solve the generalized eigenvalue problem
where H is a 3N × 3N symmetric matrix of second derivatives of the potential 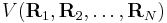 . H is the Hessian matrix of V in the equilibrium
. H is the Hessian matrix of V in the equilibrium 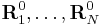 . The diagonal matrix M contains the masses on the diagonal. The diagonal matrix
. The diagonal matrix M contains the masses on the diagonal. The diagonal matrix 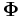 contains the eigenvalues, while the columns of C contain the eigenvectors.
contains the eigenvalues, while the columns of C contain the eigenvectors.
It can be shown that the invariance of V under simultaneous translation over t of all nuclei implies that vectors T = (t, ... , t) are in the kernel of H. From the invariance of V under an infinitesimal rotation of all nuclei around s, it can be shown that also the vectors S = (s x R10, ..., s x RN0) are in the kernel of H :
Thus, six columns of C corresponding to eigenvalue zero are determined algebraically. (If the generalized eigenvalue problem is solved numerically, one will find in general six linearly independent linear combinations of S and T). The eigenspace corresponding to eigenvalue zero is at least of dimension 6 (often it is exactly of dimension 6, since the other eigenvalues, which are force constants, are never zero for molecules in their ground state). Thus, T and S correspond to the overall (external) motions: translation and rotation, respectively. They are zero-energy modes because space is homogeneous (force-free) and isotropic (torque-free).
By the definition in this article, the non-zero frequency modes are internal modes, since they are within the orthogonal complement of Rext. The generalized orthogonalities: 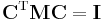 applied to the "internal" (non-zero eigenvalue) and "external" (zero-eigenvalue) columns of C are equivalent to the Eckart conditions.
applied to the "internal" (non-zero eigenvalue) and "external" (zero-eigenvalue) columns of C are equivalent to the Eckart conditions.
References
- ^ C. Eckart, Some studies concerning rotating axes and polyatomic molecules, Physical Review, vol. 47, pp. 552-558 (1935).
- ^ Aaron Sayvetz, The Kinetic Energy of Polyatomic Molecules, J. Chem. Phys. vol. 7, pp. 383-389 (1939).
- ^ L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, Addison-Wesley, Reading (1981) p. 535.
The classic work is:
- E. Bright Wilson, Jr., J. C. Decius and Paul C. Cross, Molecular Vibrations, Mc-Graw-Hill (1955). Reprinted by Dover (1980).
More advanced book are:
- D. Papoušek and M. R. Aliev, Molecular Vibrational-Rotational Spectra, Elsevier (1982).
- S. Califano, Vibrational States, Wiley, New York-London (1976). ISBN 0-471-12996-8
External links
- For a free code (developed by Z. Szabo and R. Scipioni) which calculates the vibrational frequencies starting from the Force Constant matrix in mass weighted coordinates see: Molecular Vibration